临床检验患者数据室内质量控制方法的研究进展
室内质量控制（internal quality control，IQC）为检验人员按照一定的频度连续测定稳定样品中的特定组分，并采用一系列方法进行分析，按照统计学规律推断和评价本批次测量结果的可靠程度，以此判断检验报告是否可发出，及时发现并排除质量环节中的不满意因素[1]。有效的IQC是保证实验室检测结果准确可靠的关键因素，传统的IQC是通过测定质控品，并将检测结果呈现在质控图上进行的。目前实验室广泛使用的IQC规则是由Westgard于20世纪80年代建立的多规则质控方法[2]，常用的Westgard质控规则有12s，13s，22s，R4s，41s和10x [3, 4]，实验室可根据其分析性能，选择相应的规则类型及其组合。
但是，使用质控品进行的IQC也有其缺点，例如，质控品本身可能成本较高、不稳定或难以获得；与真实的患者标本情况相比，质控品具有基质效应；用质控品进行IQC不能连续地对分析性能进行监测等[5, 6, 7, 8]。临床实验室的绝大部分误差实际上会出现在检测过程的检验前和检验后阶段，有研究表明，检验前和检验后阶段误差所占比例为93%：检验前为46%、检验中为7%、检验后为47%[3]。然而，使用质控品进行IQC只能对检验中的误差进行监测，无法确定检验前和检验后的误差。
基于患者数据的IQC则可以很好地作为传统IQC的补充，克服上述传统IQC的缺点，其最早出现在1963年发表的文献中[9]。随后，越来越多的患者数据IQC方法被提出，包括差值检查法（Delta Check）、正态均值法（Average of Normals，AoN）、Bull算法（又称移动均值法，Moving Average，MA）、指数加权移动均值法（exponentially weighted moving average，EWMA）、移动中位数法（moving median）、离群值移动和（moving sum of outliers，MovSO）与移动标准差法（moving standard deviation，MovSD）等。由于计算机技术未能得到很好的发展，导致早期的基于患者数据的IQC方法无法得到很好的应用，近些年随着信息技术的进步，这些IQC方法在实验室质量控制过程中发挥的作用也越来越大。
一、差值检查法（Delta Check）
1. 基本概念：目前，检测标本错误标识的最佳工具就是差值检查法[10]。差值检查法即一种将实验室中患者连续检测结果的差值与预先设定的控制限进行比较以对误差进行检测的临床实验室质量控制程序[11]。1974年，Nosanchuk和Gottman[12]首次提出了差值检查法的概念，用来改善临床实验室的质量控制。在原文中，作者讲述了一种人工检查患者当前和先前的检测结果，以识别不太可能出现的实验室检测结果改变的质控方法。随后，Ladenson和Whitehurst等人[13, 14]首次利用计算机将差值检查法应用于临床化学实验室中，以监测患者检测结果的变化。Wheeler和Sheiner在1981年[15]系统地比较了前述Ladenson、Whitehurst和Wheeler-Sheiner[16]的三种不同的差值检查法，认为差值检查法可以检出错误的患者检测结果，但是由于所研究人群的疾病状态或治疗的影响，也产生了很多的假阳性。
1988年，Lacher和Connelly[17]指出使用差值检查法最大的问题在于没有考虑实验室中患者连续检测之间的时间间隔，因此，两位研究者对差值检查法的基本概念进行了补充和完善，即将患者连续检测之间的时间间隔纳入差值检查法计算公式中，最终得到了4种差值检查法的基本计算方式，见表1。同时，作者建议实验室在选择相应的差值检查法计算方式时，应该考虑生物学、分析变异以及患者检测结果改变的临床相关性。
表1. 差值检查法的计算方式
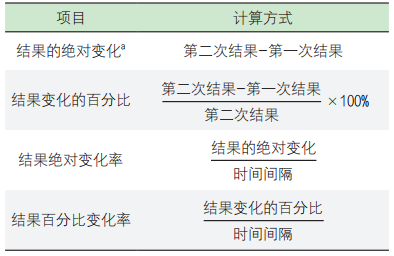
a：结果指实验室中的患者检测结果
2. 新时代的差值检查法：21世纪随着计算机技术的突飞猛进，差值检查法也得到了更多的发展。Tran及其同事[18]使用一种更加直观的3-D差值检查图来对HbA1c进行质量控制，发现这种新方法可以更好地理解、评估和比较不同的实验室患者人群；Park等人[19]也建议使用新的决策标准：根据差值与参考范围之比来选择差值检查法的计算方式；更有学者[20]创新性地将正态均值法和差值检查法相结合，利用多个连续的差值的均值来识别分析方法性能的改变，这种新的质量控制工具称为平均差值法（Average of delta，AOD），AOD可以作为IQC的一种补充，快速地对系统误差（standard error，SE）进行检测，并且适用于个体间生物学变异较大的分析物[21]。
伴随差值检查法的新进展，其在当今实验室环境下的实际作用也受到了许多质疑，例如，Strathmann等人[22]利用实验室历史数据，通过模拟的方式评估了差值检查法在识别贴错标签标本方面的性能，结果发现只有在贴错标签误差率很高的情况下差值检查法才能有效地对其检出，而且产生的差值检查警报大部分都是假阳性。作者认为实验室应该根据自己的具体情况设置差值检查法的质控规则，而不存在一个通用的规则。2012年，Ovens等人[23]利用随机动态模型模拟了钠、钾、氯化物、碳酸氢盐和肌酐等分析物的标本混乱误差，并应用差值检查法对这些误差进行检测，结果发现其阳性预测值很低。原因是由于先进技术，例如标本条形码的发展，标本混乱误差在当今实验室环境中出现的比例大大降低。Karger[24]抛出了一个疑问：使用还是不使用差值检查法？目的是告诫实验室应该评估当前使用的差值检查法参数的有效性，并回顾历史数据，以确定实验室误差是否已被有效地检出。
3. 差值检查法的应用：当差值检查法在20世纪70年代被提出时，引起差值检查法警报最常见的原因就是人工数据输入错误[13]。随着实验室信息系统（laboratory information system，LIS）和仪器设备的发展，人工参与越来越少，实际情况也随之发生变化：目前大部分差值检查法警报都和患者状态的改变以及标本错误标识相关[25]。美国临床和实验室标准化研究院（Clinical and Laboratory Standard Institution, CLSI）文件EP33给出了实验室应用差值检查法进行质量控制的流程图（图1）[10]。
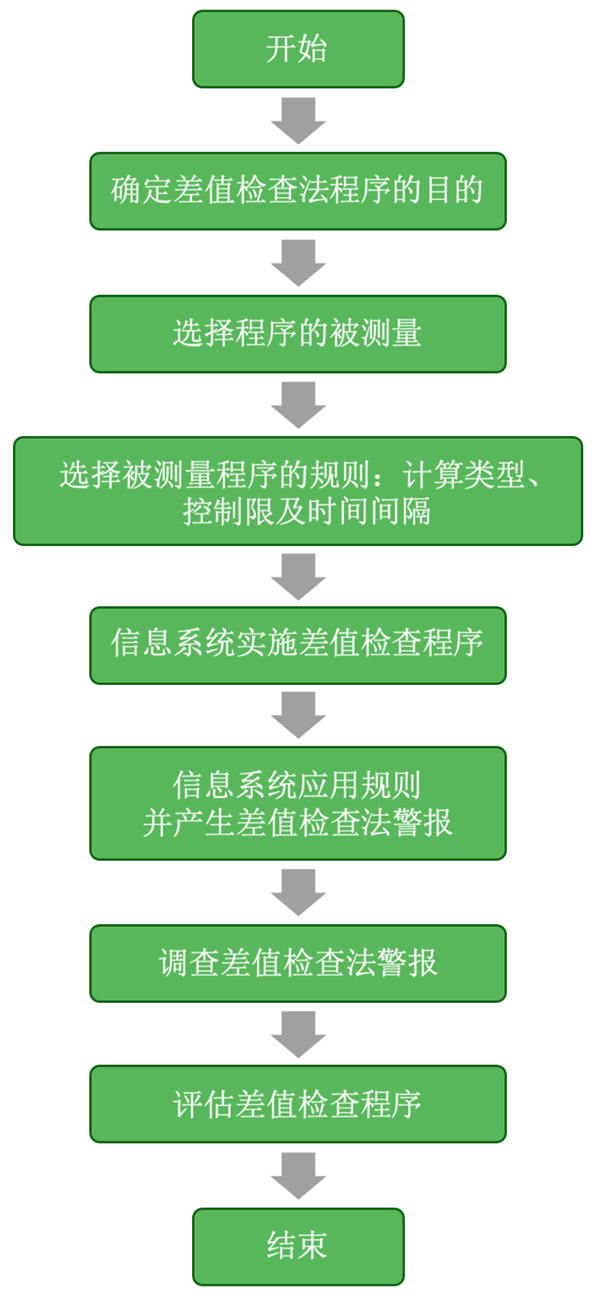
图1. 实验室差值检查法应用流程图
临床实验室可以通过查阅文献、咨询医务人员、实验室主任，甚至使用经验方法[26]，来建立适合于自己实验室的差值检查法质量控制程序。用于识别错误标识标本的分析物应该是那些在短时间内会频繁重复检测的分析物，如生化检测中的钾、钠、钙、肌酐等[10, 27]；个性指数（index of individuality）的计算方式为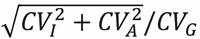
，研究表明，个性指数低（通常＜0.6）的分析物如碱性磷酸酶、血红蛋白、红细胞平均体积、红细胞平均血红蛋白含量、血小板和白细胞计数在识别错误标识标本方面也有很大作用[10, 22, 28, 29]。
实验室在选择好分析物之后，接下来的一个问题就是确定差值检查法的控制限，即实验室中患者连续检测结果之间至少多大的改变才会触发差值检查法警报，以提示实验室工作人员采取相应措施。需要注意的是，由于差值检查法的计算方式的不同，控制限可以百分比或者数值的形式进行表示。
参考变化值（Reference Change Values，RCV）是导出差值检查法控制限的方式之一[30, 31, 32]。1983年，Harris和Yasaka提出了RCV的概念[32]，其基本原理是如果个体连续检测结果的改变具有统计学意义的话，连续检测结果之间的差异必需要大于固有变异（检验前、检验中、检验后以及个体内生物学变异），相应的计算公式为[10]：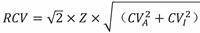
其中，CVA代表实验室的分析不精密度，取决于仪器和测量程序，可通过常规质控品的质控数据进行计算；CVI代表个体内生物学变异，可通过查阅相关文献获得[30]；Z代表统计学中的Z分数，一般可取1.96或2.58，对应的概率分别为95%和99%。
另一种设置差值检查法控制限的方法是利用实验室患者检测结果，如利用差值检查法计算结果分布的百分位数作为控制限[17, 31]，百分位数的选择也会影响差值检查法的假阳性率。Tran等人[18]的研究也建议使用基于患者人群分布的第0.5百分位数和第99.5百分位数来发现可能的分析误差和标本混乱。
二、正态均值法（Average of Normals，AoN）
1965年，Hoffman和Waid[33]提出了一种使用患者标本来进行实验室质量控制的新方法，其基本过程可以分为以下两步：1. 在每天的结束时，将落在正常范围内的患者检测结果进行平均；2. 将得到的“正态均值”描在质控图上。但是，Amador和Owen[34, 35]的研究均表明正态均值法在检测系统误差的能力方面不如传统质量控制程序。Owen还指出：由于患者检测结果之间存在很大的变异，因此不可能使用患者结果质量控制方法来检测随机误差。Reed等人[36]在进行研究后，对正态均值法提出了两点修改建议：1.使用相同数目的患者检测结果来计算均值；2. 基于结果分布而非参考区间设置截断界限。Bgetrup等人[37]则认为一部分检测项目的正态均值法可以用来对系统误差进行监测，也可以用来对分析水平的稳定性进行定期检查，是对传统IQC的一种很好的补充。
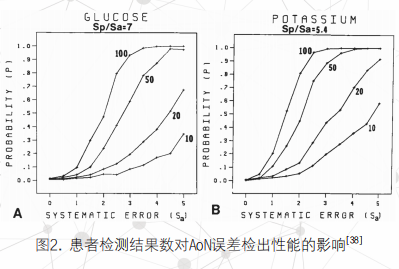
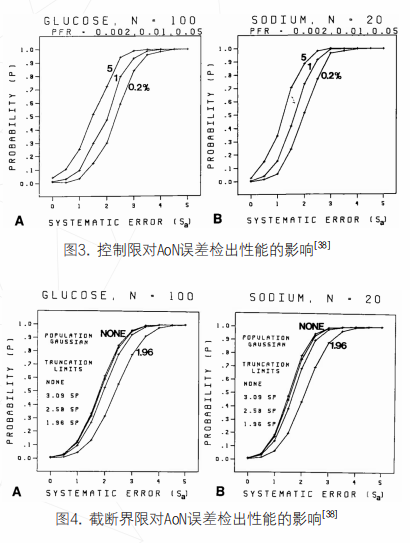
1984年，Cembrowski和Westgard等人[38]利用功效函数图[39]充分研究了影响AoN程序能力的几个重要参数，包括患者人群标准差（sp）与分析标准差（sa）之比，即sp/sa、用来计算均值的患者检测结果数（N）、控制限（假失控概率）、截断界限和位于截断界限之外的人群大小：随着sp/sa减小，在相同的功效下，N的值越小；随着控制限变窄，假失控概率上升，误差检出概率也会增加；没有离群值存在的情况下，最宽的截断界限可以提供最大的误差检出概率；随着离群人群比例的增加，误差检出功效在下降，图2-4展示了文献中AoN的功效函数图模拟结果。作者表示，对于有稳定质控品的分析方法来说，AoN程序目前只能作为一种补充，建立AoN方法的步骤为[7]：
1. 收集连续几周的患者数据，并用计算机画出数据的频数直方图。
2. 使用中央区域的数据，计算患者标本数据的平均值 p和sp；
3. 从质控物确定分析标准差（sa），质控物的平均浓度应接近患者标本数据的平均值；
4. 由公式Np=2×Nc×（sp/sa）2 估计Np或从基于sp/sa和检出∆SEC概率的关系图中得到Np。
5. 选择患者测定值的截断界限（通常为±3.09sp,±2.58sp或±1.96sp）。
6. 选择控制限使Pfr不超过1%，通常为 p±3.09×sp/√Np或 p±2.58×sp/√Np。
Ichihara等人[40]探究了AoN质控方法在放射免疫分析中的质量控制作用，发现良好性能的AoN方法需要满足以下两个条件：1. 患者测量结果分布模式不变；2. 异常数据的比例不能太大。1996年，Westgard等人[41]探讨是否可以通过AoN算法对批长度进行监测，在作者所研究的38个检测项目中，发现大约有一半的检测项目在应用AoN算法监测批长度方面有很大的潜力。Aslan等人[42]应用AoN对实验室20项临床化学试验进行质量控制，并说明对于昂贵的传统IQC来说，AoN是一个很好的补充，尤其是对于工作量很大的大型医院实验室来说。
尽管一些研究已经从理论层面对AoN进行了详细的描述[43]，但是要选择特定检测项目的AoN质控程序，并不是一件简单的事，需要综合考虑所研究的患者人群和分析方法本身的性质（例如，患者人群均值、标准差和分析标准差等等）。van Rossum等人使用偏倚检测曲线和确认图对肌酐[44]、24个常规化学检测[45]的AoN程序进行优化，发现优化后的AoN程序可快速检测到分析误差，并且假失控数量也能维持在一个可控水平。
三、移动均值法（Moving Average，MA）
1. Bull算法（Bull Algorithm）：Bull算法是由Bull等人[46]于1974年提出的一种利用患者红细胞指数（red blood cell indices）进行血液学质量控制的方法，又称为移动均值法（Moving Average，MA），本质上是正态均值法[3]。利用Bull算法进行质量控制的理论依据是血液红细胞计数可因稀释、浓缩、病理性或技术性因素而有明显的增减，但每个红细胞的体积，及其所含的血红蛋白，或单位红细胞容积中所含有的血红蛋白则相对稳定，几乎不受这些因素的影响，根据这种特性，设计监测平均红细胞体积（MCV）、平均红细胞血红蛋白含量（MCH）和平均红细胞血红蛋白浓度（MCHC）的均值变动，来进行质量控制[7, 47]。原文中，Bull等人也提出了实施这个方法的步骤：1. 累积N个患者的MCV、MCH和MCHC的检测结果；2. 估计每个红细胞指数的均值；3. 比较已知人群均值（μ）和估计计算得到的均值之间的差异，以确定是否需要对常规实验室操作进行检查。
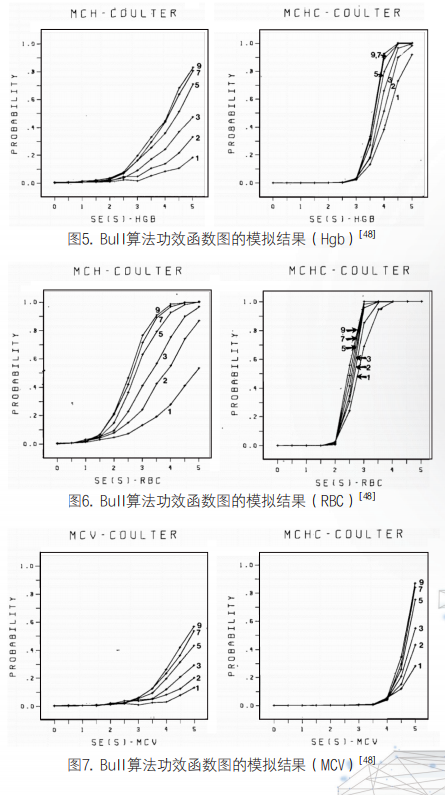
随后，Cembrowski和Westgard等人[48]利用计算机模拟和功效函数图的方式对Bull算法进行了评估，认为Bull算法能够有效地检测出较大的误差，并且其误差检出性能随着分析批数目的增加而增加，图5-7展示了文献中Bull算法的功效函数图模拟结果。作者还比较了Bull算法质控和常规质控品质控程序，发现质控品的多规则程序对2倍标准差大小的系统误差的误差检出概率为60%，但是Bull算法对相同误差的误差检出概率却接近于0。此外，使用患者数据进行质量控制的Bull算法无法检出随机误差。Levy等人[49]指出了Cembrowski和Westgard等人研究中的缺陷：Bull算法质控和常规质控品质控的比较并未建立在平等的基础之上，前者只是利用单个的Bull均值作为统计量，而后者利用的则是多规则质控方法。因此，作者提出了多规则Bull算法，以完善Bull算法质控和常规质控品质控的比较。最后作者发现，在使用相似的质控规则的情况下，两种质控方法对系统误差的误差检出概率很接近。随后，Lunetzky等人[50]对Levy及其同事提出的多规则Bull算法进行了评估。在这个程序中，只要满足下列标准之一，则判定一批患者标本失控：1. 红细胞指数中一个Bull均值超出其3%控制限；2. 三个连续的Bull均值平均数超出其2%控制限。评估结果显示：多规则Bull算法的误差检出能力优于以3%作为控制限的单个Bull均值的Bull算法。
2. 指数加权移动均值法（exponentially weighted moving average，EWMA）：最早，EWMA控制图是在制造业中由Roberts[51]提出的，1975年，Cembrowski和Westgard等人首次将指数修匀的概念引入临床化学实验室。与休哈特控制图不同的是，EWMA控制图也使用了先前的值，其思想是将来自先前批次的控制测定值与当前批次的控制测定值相结合，以更有效地估计系统误差[52]。
Neubauer[53]详述了EWMA的基本过程：将当前测定值与加权因子ω相乘，再将其与用（1-ω）进行加权的所有先前测定值的总和相加，因此，在每个时间t（t=1,2…），就可以获得一个检验统计量zt（zt=ω t+（1-ω）×zt-1），随着时间的推移，将计算所得zt值表示在控制图上。由于 t=（x1t+x2t+⋯+xnt）/n（n为每批的控制测定值），因此这种控制图叫做EWMA-zt控制图，其另外一种表达方式为zt=ω∑ （1-ω）i t-i+（1-ω）tz0，其中，z0设定为先前质控观测值的均值，加权因子ω∈（0,1）[54]。同时，作者还将EWMA控制图与Westgard多规则质控图进行了比较，发现两者在偏倚的检测方面能力相同，在不精密度的质量控制方面，EWMA控制图的能力则较差。但是，EWMA质控图的优点是可以检测到小的改变，因此其可以作为传统多规则质控的一个补充。
3. 广义的移动均值法：（1）移动中位数法（moving median）：在实验室实际的质量控制工作中，患者的检测结果可能会存在很大的变异，结果的分布可能会呈现明显的偏斜，而非正态分布，尤其是对于大型综合医院来说，由于科室众多，患者来源复杂，患者检测结果变异的现象会更加明显，这非常不利于传统移动均值法在实验室质量控制中的应用。类比于移动均值法，Wilson等人在自己实验室的质控程序中使用了一种移动中位数法来检测分析方法性能的改变和变化趋势。移动中位数法不易受分布中离群值的影响，在实验室患者检测结果呈偏态分布的情况下，中位数比均值更加稳定[55, 21]，这在实际的实验室工作中具有一定的优势。随后，Fleming等人在自己的实验室内采用实时的患者数据质控，计算统计量移动中位数和移动均值，持续地对检测过程进行监测，并取得显著成效[56]。关于移动中位数法的研究相对较少，目前此方法比较难解决的两个问题是：1. 相对于传统的L-J质控图，对移动中位数法质控结果的解释更加困难，具有主观性[5]；2. 中位数的标准差难以估计，Wilson等人通过其与均值标准差之间的数学关系来进行计算，计算公式为Var[Median]/Var[Mean]=π/2，其中Var代表统计学中的方差[55]。（2）离群值移动和（moving sum of outliers，MovSO）与移动标准差法（moving standard deviation，MovSD）：前述所有基于患者数据的质量控制方法大多对不精密度（随机误差）的控制能力较弱，Liu等人[57]建立的离群值移动和与移动标准差法则可以弥补这个不足。离群值移动和将固定数量的连续检测结果（区块）内的离群值（落在参考区间外的检测结果）数目作为一个移动统计量来进行计算，并可将此统计量描在质控图上，其控制限可表示为均值±3标准差，需要注意的是，此表达式的均值指的是稳定时期若干区块范围内的离群值的平均数目，标准差则是通过离群值数目计算所得的标准差。移动标准差法即将移动均值法中的均值替换为标准差的计算，而上下控制限的计算则更加复杂。实际上，不管是离群值移动和还是移动标准差法，其本质上都是一种更加广泛的移动均值法[58]，符合移动均值法的基本特征：截断界限、计算算法和控制限，其中计算算法并不拘泥于“均值”的计算。ANPed定义为误差检出前受影响的患者结果平均数，与传统室内质控和AoN相比，离群值移动和与移动标准差法的共同特点是可以有效地检出逐渐增加的随机误差，尤其是对于生物学变异较小的分析物来说（（CVi2+CVg2）/CVa2＜10），同时还可以显著降低ANPed[57]。
四、总结
距离基于患者数据质量控制方法的提出已有半个世纪之久，早期由于实验室信息学发展的不完善以及相关软硬件的缺乏，使得相关的研究较少，加之患者数据质量控制方法本身对统计学的要求较高、极易受患者人群分布的影响并且需要相对较多的实验室患者检测结果数量，更加阻碍了患者数据质量控制方法在实验室中的普及，到目前为止，仍然缺乏相关的标准指南和建议。CLSI文件EP33[10]的开头就如是说：“尽管差值检查法在一些实验室已经使用超过40年，但在同行评议的科学文献中很少有关于差值检查法的用途和目的的描述。”但是，作为一种利用患者标本检测结果的质量控制方法，其更加符合真实的实验室情况和患者人群分布，因此无基质效应、无互换性等问题；在实验室的日常工作中，患者标本不断地被检测，就不断地产生新的患者检测结果，因此基于患者数据的质量控制也可以持续不断地进行下去，做到实时质控，甚至可以与患者的临床状态直接相关。精心设计的患者数据质量控制方法更可以帮助实验室了解自己实验室特定检测项目的生物学和分析特性以及所针对的患者人群情况。因此，患者数据质量控制方法是一种更加个性化的质量控制方法，给实验室提供了另一种质控思路。借助计算机，实验室可以同时利用质控品和患者数据进行质量控制，两者相辅相成，共同提高实验室检验结果的准确性和整体质量水平。
参考文献
中华人民共和国国家卫生健康委员会. WS/T 641-2018. 临床检验定量测定室内质量控制[S]. 北京:中国标准出版社, 2018
Westgard JO, Barry PL, Hunt MR, et al. A multi-rule Shewhart chart for quality control in clinical chemistry [J]. Clin Chem. 1981;27(3):493-501.
Kazmierczak SC. Laboratory quality control: using patient data to assess analytical performance [J]. Clin Chem Lab Med. 2003;41(5):617-627.
Westgard JO. Internal quality control: planning and implementation strategies [J]. Ann Clin Biochem. 2003; 40 (Pt 6):593-611.
Badrick T, Cervinski M, Loh TP. A primer on patient-based quality control techniques [J]. Clin Biochem. 2019;64:1-5.
Badrick T, Bietenbeck A, Cervinski MA, et al. Patient-Based Real-Time Quality Control: Review and Recommendations [J]. Clin Chem. 2019;65(8):962-971.
王治国. 临床检验质量控制技术[M].第3版. 北京:人民卫生出版社, 2014.
Loh TP, Cervinski MA, Katayev A, et al. Recommendations for laboratory informatics specifications needed for the application of patient-based real time quality control [J]. Clin Chim Acta. 2019;495:625-629.
DORSEY DB. QUALITY CONTROL IN HEMATOLOGY [J]. Am J Clin Pathol. 1963;40:457-464.
CLSI. Use of Delta Checks in the Medical Laboratory (1st Edition) [S]. CLSI guideline EP33.Wayne, PA: Clinical and Laboratory Standards Institute; 2016.
Tan RZ, Markus C, Loh TP. Impact of delta check time intervals on error detection capability [J]. Clin Chem Lab Med. 2020;58(3):384-389.
Nosanchuk JS, Gottmann AW. CUMS and delta checks. A systematic approach to quality control [J]. Am J Clin Pathol. 1974;62(5):707-712.
Ladenson JH. Patients as their own controls: use of the computer to identify "laboratory error" [J]. Clin Chem. 1975;21(11):1648-1653.
Whitehurst P, Di Silvio TV, Boyadjian G. Evaluation of discrepancies in patients' results--an aspect of computer-assisted quality control [J]. Clin Chem. 1975;21(1):87-92.
Wheeler LA, Sheiner LB. A clinical evaluation of various delta check methods [J]. Clin Chem. 1981;27(1):5-9.
Wheeler LA, Sheiner LB. Delta check tables for the Technicon SMA 6 continuous-flow analyzer [J]. Clin Chem. 1977;23(2 PT. 1):216-219.
Lacher DA, Connelly DP. Rate and delta checks compared for selected chemistry tests [J]. Clin Chem. 1988;34(10):1966-1970.
Tran DV, Cembrowski GS, Lee T, et al. Application of 3-D Delta check graphs to HbA1c quality control and HbA1c utilization [J]. Am J Clin Pathol. 2008;130(2):292-298.
Park SH, Kim SY, Lee W, et al. New decision criteria for selecting delta check methods based on the ratio of the delta difference to the width of the reference range can be generally applicable for each clinical chemistry test item [J]. Ann Lab Med. 2012;32(5):345-354.
Jones GR. Average of delta: a new quality control tool for clinical laboratories [J]. Ann Clin Biochem. 2016; 53(Pt 1): 133-140.
Liu J, Tan CH, Badrick T, Loh TP. Moving sum of number of positive patient result as a quality control tool [J]. Clin Chem Lab Med. 2017;55(11):1709-1714.
Strathmann FG, Baird GS, Hoffman NG. Simulations of delta check rule performance to detect specimen mislabeling using historical laboratory data [J]. Clin Chim Acta. 2011;412(21-22):1973-1977.
Ovens K, Naugler C. How useful are delta checks in the 21 century? A stochastic-dynamic model of specimen mix-up and detection [J]. J Pathol Inform. 2012;3:5.
Amy B. Karger. To Delta Check or Not to Delta Check? That Is the Question [J]. J Appl Lab Med.2017;4(1):457-459.
Straseski JA, Strathmann FG. Patient data algorithms [J]. Clin Lab Med. 2013;33(1):147-160.
Schifman RB, Talbert M, Souers RJ. Delta Check Practices and Outcomes: A Q-Probes Study Involving 49 Health Care Facilities and 6541 Delta Check Alerts [J]. Arch Pathol Lab Med. 2017;141(6):813-823.
Tan RZ, Markus C, Choy KW, et al. Optimized Delta Check Rules for Detecting Misidentified Specimens in Children [published online ahead of print, 2019 Dec 31]. Am J Clin Pathol. 2019;aqz201.
Randell EW, Yenice S. Delta Checks in the clinical laboratory [J]. Crit Rev Clin Lab Sci. 2019;56(2):75-97.
Fu Y, Luo G, Tang Z, Li M, Chen S, Jiang H. Clinical validation of a delta check model in haematology automated counting improves data validation [J]. Int J Lab Hematol. 2020;42(1):77-81.
Lee J, Kim SY, Kwon HJ, et al. Usefulness of biological variation in the establishment of delta check limits [J]. Clin Chim Acta 2016;463:18-21.
Ko DH, Park HI, Hyun J, et al. Utility of Reference Change Values for Delta Check Limits [J]. Am J Clin Pathol. 2017;148(4):323-329.
Harris EK, Yasaka T. On the calculation of a "reference change" for comparing two consecutive measurements [J]. Clin Chem. 1983;29(1):25-30.
HOFFMANN RG, WAID ME. THE "AVERAGE OF NORMALS" METHOD OF QUALITY CONTROL [J]. Am J Clin Pathol. 1965; 43: 134-141.
Amador E, Hsi BP, Massod MF. An evaluation of the "average of normals" and related methods of quality control [J]. Am J Clin Pathol. 1968;50(3):369-378.
Owen JA, Campbell DG, Fenwick D, et al. Laboratory quality control using patients results. Clin Chim Acta. 1968; 20(2):327-334.
Reed AH. Use of patient data for quality control of clinical laboratory tests[J]. Clin Chem. 1970; 16(2): 129-134.
Begtrup H, Leroy S, Thyregod P, et al. 'Average of normals' used as control of accuracy, and a comparison with other controls [J]. Scand J Clin Lab Invest. 1971;27(3):247-253.
Cembrowski GS, Chandler EP, Westgard JO. Assessment of "Average of Normals" quality control procedures and guidelines for implementation [J]. Am J Clin Pathol. 1984;81(4):492-499.
Westgard JO, Groth T. Power functions for statistical control rules [J]. Clin Chem. 1979;25(6):863-869.
Ichihara K, Miyai K, Takeoka K, et al. Distribution of patients' test values and applicability of "average of normals" method to quality-control of radioimmunoassays [J]. Am J Clin Pathol. 1985;83(2):206-210.
Westgard JO, Smith FA, Mountain PJ, et al. Design and assessment of average of normals (AON) patient data algorithms to maximize run lengths for automatic process control [J]. Clin Chem. 1996;42(10):1683-1688.
Aslan D, Kuralay F, Tanyalsin T, et al. Use of averages of patient data for quality control [J]. Accred Qual Assur, 1999, 4(9-10):431-433.
Carey RN. Patient population controls [J]. Clin Lab Med. 2013;33(1):139-146.
van Rossum HH, Kemperman H. A method for optimization and validation of moving average as continuous analytical quality control instrument demonstrated for creatinine [J]. Clin Chim Acta. 2016;457:1-7.
Rossum HHV, Kemperman H. Implementation and application of moving average as continuous analytical quality control instrument demonstrated for 24 routine chemistry assays [J]. Clin Chem Lab Med. 2017;55(8):1142-1151.
Bull BS, Elashoff RM, Heilbron DC, et al. A study of various estimators for the derivation of quality control procedures from patient erythrocyte indices [J]. Am J Clin Pathol. 1974;61(4):473-481.
Ali SA, Shaikh MS. Better get moving on laboratory quality assurance [J]. Int J Health Care Qual Assur. 2019;32(1):84-86.
Cembrowski GS, Westgard JO. Quality control of multichannel hematology analyzers: evaluation of Bull's algorithm [J]. Am J Clin Pathol. 1985;83(3):337-345.
Levy WC, Hay KL, Bull BS. Preserved blood versus patient data for quality control--Bull's algorithm revisited [J]. Am J Clin Pathol. 1986;85(6):719-721.
Lunetzky ES, Cembrowski GS. Performance characteristics of Bull's multirule algorithm for the quality control of multichannel hematology analyzers [J]. Am J Clin Pathol. 1987;88(5):634-638.
Roberts SV. Control chart tests based on geometric moving averages [J]. Technometrics 1959;1:239-250.
Linnet K. The exponentially weighted moving average (EWMA) rule compared with traditionally used quality control rules [J]. Clin Chem Lab Med. 2006;44(4):396-399.
Neubauer AS. The EWMA control chart: properties and comparison with other quality-control procedures by computer simulation [J]. Clin Chem. 1997;43(4):594-601.
Lukić V, Ignjatović S. Optimizing moving average control procedures for small-volume laboratories: can it be done? [J]. Biochem Med (Zagreb). 2019;29(3):030710.
Wilson A, Roberts WL, Pavlov I, Fontenot J, Jackson B. Patient result median monitoring for clinical laboratory quality control [J]. Clin Chim Acta. 2011;412(15-16):1441-1446.
Fleming JK, Katayev A. Changing the paradigm of laboratory quality control through implementation of real-time test results monitoring: For patients by patients [J]. Clin Biochem. 2015;48(7-8):508-513.
Liu J, Tan CH, Badrick T, Loh TP. Moving standard deviation and moving sum of outliers as quality tools for monitoring analytical precision [J]. Clin Biochem. 2018;52:112-116.
van Rossum HH. Moving average quality control: principles, practical application and future perspectives [J]. Clin Chem Lab Med. 2019;57(6):773-782.
王薇主编, 临床检验质量指标-室内质量控制和室间质量评价，人民卫生出版社，2020.
