测量误差理论与术语定义的 发展与变化

测量是人类认识自然、探索自然必不可少的一种重要手段。由于多种因素的影响，在测量过程中必然存在误差，通过对误差产生原因的分析可有效地减小或消除误差，从而提高测量水平，在最经济的条件下获取最理想的测量结果，因此，误差理论和数据处理的重要性得到了越来越广泛的认同。特别是在当今信息技术时代，任何科学实验和工程实践所获得的数据信息，必须经过合理的数据处理并给出科学的评价，才具有实际价值[1]。

由测量误差的定义、分类、分布、估计、数据处理和实验标准偏差等概念，形成了测量误差理论体系[2]，为测量数据准确度和可靠性的评定奠定了坚实的理论基础。

误差理论的发展已有200多年历史，国际计量标准也随之变化，我国的计量技术规范也要与国际标准一致并随之变化。本文总结了测量误差理论的发展历程与发展方向，回顾了与误差理论和数据处理相关的国家计量技术规范随国际计量技术规范的发展而发展的过程，分析了国家计量技术规范中测量误差、系统误差、随机误差和不确定度等主要误差术语定义的变化情况和变化趋势，以便对误差理论有系统全面的认识，掌握测试与实验数据处理的基本理论与方法，正确估计被测量的值，科学客观地评价测量结果，并根据测试对象的精度要求，对测试与实验方法进行合理设计。

1 误差理论的发展

误差理论的研究随着生产与科技的发展而前进，总体上可分为经典和现代误差理论两个阶段[3]。经典误差理论以统计理论为基础，主要以随机误差为对象进行数据处理。现代误差理论包括测量不确定度原理及应用、误差修正技术和动态测量误差评定等内容，以实用性为特征。初期的经典误差理论认为误差就是单一的随机误差。但有许多学者发现影响测量准确度的因素除了随机误差，还有其他因素，故提出误差的可分性，将误差分为随机误差、系统误差和粗大误差3类，给出了不同的处理方法，即剔除粗大误差、修正系统误差，并用随机误差统计参量来评定测量结果的精度。从误差的单一性发展到误差的可分性，这是误差理论的重要进展，测量数据处理的科学性和误差评定的可靠性明显提高。

20世纪中期，误差转化和误差合成是误差理论的又一次重要进展[3]。误差转化是指在一定条件下, 某些随机误差和系统误差可以互相转化。系统误差被划分为已定系统误差和未定系统误差，并给出不同处理方法，即对已定系统误差进行修正，而对未定系统误差则与随机误差一起计入测量结果的精度评定。误差合成是指在测量结果的精度评定中必须包含随机误差、转化后的随机误差和只知误差限的未定系统误差，并用一个误差数值来表示这些误差。

1970年前后，一些学者开始用不确定度来评定测量结果的可靠性，但国际上对不确定度的理解和表示方法缺乏一致性。1980年，国际计量局提出了《实验不确定度表示建议书IN C-1》。1986年，国际标准化组织等7个组织共同制定了《测量不确定度表示指南》。1993年，该指南由国际标准化组织颁布实施，在世界各国广泛执行[1] 。测量不确定度的应用是误差理论发展的重要里程碑，也是现代误差理论的重要内容之一。“建议书”具有科学性和实用性特点，对统一国际间的测量精度评定起着积极推动作用。其科学性主要是给出的测量不确定度全面地考虑了测量准确度的各种误差因素；其实用性在于比较容易判别两类不确定度评定。

现有的误差理论都是针对静态测量，而对测量随时间变化的动态测量尚无科学的评定理论。目前，常用静态测量理论来近似地代替动态测量理论或采用随机过程特征量参数来评定动态测量结果，都是近似方法，与实际情况还有明显差距。因此，对动态测量误差的评定还需要进行深入研究，这也是现代误差理论的发展方向。

2 我国计量技术规范的发展

计量和测量关系十分密切。测量是为了通过全部操作获得量值，而计量是实现单位统一和量值准确可靠的活动[4]。计量保证了测量的统一和准确一致, 统一首先在单位上，准确一致反映在量值上[5]。两者在很大范围内具有相同的含义，但并不等同。计量除包括所有物理量、化学量和生物量的测量以外，还包括了管理与科研工作，测量中也有一些内容与计量无关[6]。

新中国成立前，我国的计量工作处于非常落后的状态。1955年，我国成立了国务院直属的国家计量局；1959年，国务院发布了《关于统一计量制度的命令》和《统一公制计量单位名称方案》，使长期以来存在的计量单位名称各异、使用计量单位和计量器具不规范的混乱局面初步得到抑制。1985-09-06，六届人大常委会第十二次会议审议通过了《计量法》[7]。

目前，我国实施的国家计量技术规范中与测量误差有关的内容主要有2个方面。

(1) 规范计量名词术语及定义。这是计量工作的一项基础性建设。1982-05-17，国家计量局批准颁布了《JJG 1001-82常用计量名词术语及定义（试行）》，并于当年10月起实施[8]。这是我国制定的第一个国家计量技术规范。

1984年, 由国际计量局、国际电工委员会、国际标准化组织及国际法制计量组织联合制定的《国际通用计量学基本名词》（简称《VIM》）一书出版, 在国际范围内统一了计量学的通用名词术语。为进一步参照《VIM》，并结合我国国情完善我国的计量名词术语，1990年，国家技术监督局计量司对《JJG 1001-82常用计量名词术语及定义(试行)》进行了修订，采用新的国际计量术语，解决定义计量、测量及其英文译文问题，同时结合我国实际使用的需要，扩大计量名词的范围。1991-01-12，国家技术监督局批准颁布了《JJG 1001) 91 通用计量名词及定义》，收录的计量名词由1982年版本的100条增加到210条[9] ，于1991-10-01起实施。

1993年，国际计量局、国际标准化组织等7个国际组织颁布了《VIM》第2版，国际法制计量组织亦于1995年提出了《法制计量学名词》（简称《VML》）新草案。为更好地与国际接轨，1998-09-16，国家技术监督局批准颁布《JJF 1001-1998通用计量术语及定义》，收录了5VIM6中全部120个名词，选用了《VML》中31个主要名词，技术规范代号改为JJF，于1999-03-01起实施[4]。

2007-02-06，国际标准化组织正式颁布了《VIM》第3版，国际法制计量组织也颁布了《VML》第3版，同时，质量监督检验检疫总局（简称国家质检总局）配合全国科学技术名词审定委员会制定了《计量学名词》，使得计量术语及定义规范的修订工作迫在眉睫。2009年3月国家质检总局组织成立了《通用计量术语及定义》国家计量技术规范修订起草小组，确定了与《VIM》和《VML》术语定义保持一致的修改原则。目前，修订工作正在进行中[5]。

(2) 制定有关测量误差评定的规范。1991-08-05，国家技术监督局批准发布了《JJF 1027-91测量误差及数据处理》，于1992-10-01起实施[10]。该规范主要包括测量结果的误差评定和计量器具准确度的评定两方面内容，对测量误差和数据处理中常遇到的一些问题做出了统一规定，以便正确地给出和使用测量结果[11]。

1993年，国际标准化组织颁布并在全世界实施了《测量不确定度表示指南》，我国也积极响应。1999-01-11，国家质量技术监督局批准发布了《JJF 1059-1999 测量不确定度评定与表示》，于1999-05-01起实施。该规范代替了《JJF 1027-91测量误差及数据处理》中的测量误差部分，给出了在常见情况下，评定与表示测量不确定度的原则、方法和简要步骤[12]。

2002-11-04，国家质量技术监督局批准发布《JJF 1094-2002测量仪器特性评定技术规范》，代替《JJF 1027-91测量误差及数据处理6中的计量器具准确度评定部分，于2003-02-04起实施[6]。

3 误差术语定义变化

3. 1 测量误差

测量误差（简称误差）的定义从20世纪70年代到2007年都没有改变，其定义为测量结果减被测量的真值[4]。

测量结果是由测量所得到的赋予被测量的值[4]。《JJF 1001-1998 通用计量术语与定义》在注中明确：在给出测量结果时，应说明它是示值、未修正测量结果或已修正测量结果，还应表明它是否为几个值的平均。在测量结果的完整表述中应包括测量不确定度，必要时还应说明有关影响量的取值范围[4]。这个注解里测量结果的含义较多，在误差的定义里，测量结果应该是示值、未修正测量结果，而不是其他。

真值是与给定的特定量的定义一致的值[4]，只有通过完善的测量才有可能获得。由于不存在完美的测量方法、条件和仪器，因此，量的真值是理想的概念，人们可以逐步接近它，但只能是近似或估计，本质上真值是不能确定的，实际上用的是约定真值。约定真值有时称为指定值、最佳估计值、约定值或参考值[4]。常用某量的多次测量结果来确定约定真值。因而，作为测量结果与真值之差的测量误差，是无法准确得到的。测量结果的误差由若干分量组成，是全部分量的代数和。在《JJG 1027-91测量误差及数据处理》里，把误差分为系统误差、随机误差和粗大误差3类。但在《JJF 1001-1998通用计量术语与定义》里，则取消了粗大误差；误差按其特性被分成随机误差与系统误差，这是因为考虑到粗大误差是由于测量条件意外改变或测量人员的主观原因等非正常情况的错误所导致的，含有这种错误的观测值应剔除，而不应参与数据的处理。

2007年，《VIM》第3版对测量误差有了新的定义：测得量值减参考量值[2]。新定义用“测得量值”代替了“测量结果”，用“参考量值”代替了“真值”。测得量值也称测得值，是表示测量结果的量值。该表述更加准确，指的是示值或未修正测量结果，而不是用测量列均值和测量不确定表述的测量结果或已修正的测得值。参考量值也称参考值，可以是被测量的真值、约定真值或标准量值。同原定义相比，新定义增加了参考量值也可以是标准量值的含义。故测量误差的新旧定义本质是一致的，新定义避免了概念的模糊，更加合理准确，增强了测量误差的科学性和可操作性。

3. 2 系统误差

《JJG 1001-91通用计量名词及定义》中系统误差的定义为：在同一被测量的多次测量过程中，保持恒定或以可预知方式变化的测量误差分量。《JJG 1027-91测量误差及数据处理6中系统误差的定义相同，且按其变化规律分为: ① 固定值的系统误差。其值（包括正负号）恒定。② 随条件变化的系统误差。其值以确定的，并通常是已知的规律随某些测量条件变化。上述定义中，系统误差的性质是“恒定”和“可预知”，特点明确，在实际操作中较易掌握。

1993年《VIM》第2版中系统误差的定义有了原则性的改变，故在《JJF 1001-1998通用计量名词及定义》中其定义为：在重复性条件下，对同一被测量进行无限多次测量所得结果的平均值与被测量的真值之差。该定义排除了系统误差的可预知性，而肯定了在多次重复中不能相互抵消的部分为系统误差[13]。由于只能进行有限次数的重复测量，真值只能用给定真值代替，该定义的可操作性不强，所得到的系统误差只是个估计值。

2007年的《VIM》第3版对系统误差的定义又有了变化：在重复测量时保持恒定不变或按可预见的方式变化的测量误差分量[2]。该定义与《JJG 1001-91通用计量名词及定义》的定义极为相似，与1998年的定义相比，特点更清楚，可操作性更强。确定了系统误差的恒定值或变化规律，就要将其作为修正值以补偿或减少误差的影响。

3. 3 随机误差

《JJG 1001-91通用计量名词及定义》和《JJG 1027-91测量误差及数据处理》中随机误差的定义为：在同一量的多次测量过程中，以不可预知方式变化的测量误差分量。它引起对同一量的测量列中各次测量结果之间的差异，常用标准差表征。这一定义强调随机误差的出现是不可预知的，其值的大小以及其正负号均不可预知。既然不可预知就无法确定随机误差存在所谓对称性、有界性和单峰性。因此，计量学界提出把随机误差称为“偶然误差”，其具有对称性。

1993年，《VIM》第2版中随机误差的定义有了本质上的改变。在《JJF 1001-1998通用计量名词及定义》中，其定义为：随机误差是指测量结果与在重复性条件下, 对同一被测量进行无限多次测量所得结果的平均值之差[4]。这个定义中不再提随机误差的不可预知，而是明确规定随机误差等于误差减去系统误差。不再有偶然误差这一术语，也不再有其他定义。同样地，因为不可能进行无限多次测量，该定义的操作性不强。根据误差、系统误差和随机误差的定义，它们有如图1所示的关系。图1中，设测得值呈正态分布N（μ，σ2），其中，μ为总体均值，σ为标准误差，被测量值为x，其真值为t，无限多次测量所得结果的平均值即总体均值为μ，第i次测量的测得值为xi，实际测量中只能进行有限次数的测量，测量列的均值为x。

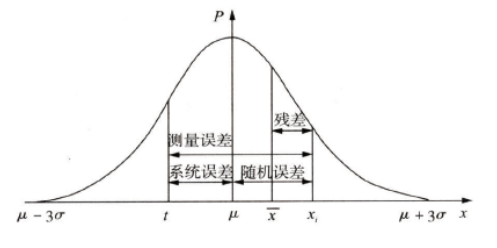
图1 测量值的概率密度分布曲线图

由图可见，误差和测量值的概率分布密切相关，可以用概率论和数理统计的方法来恰当处理。

2007年《VIM》第3版中随机误差的定义为：在重复测量时按不可预见的方式变化的测量误差的分量[2]。该定义明确了随机误差的特性是不可预知的，具有可操作性。

根据定义，在实际测量中操作如下：在相同条件下重复做实验，大小和正负都没有规律的误差就是随机误差。对同一被测量，若改变实验条件重复做实验，出现的恒定不变或有明确变化规律的误差就是系统误差。

3. 4 不确定度

测量误差与测量不确定度是误差理论中两个最重要的概念。测量误差是测量结果偏离真值的差值，不能用它来定量表明测量结果的可靠程度，它是计算测量不确定度的基础。测量不确定度反映测量所得量值不能肯定的程度，是表示被测量的量值分散性的量度，是一个区间，说明了测量结果中可能出现的误差限。

测量不确定度最初的定义是：由测量结果给出的被测量估计值的可能误差的度量, 表征被测量的真值所处范围的评定[9]。《JJG 1027-91测量误差及数据处理》中规定：用统计学方法评定的不确定度是A类不确定度，用非统计学方法评定的不确定度是B类不确定度。总不确定度用于测量结果报告，又称报告不确定度。

《JJF 1001-1998通用计量名词及定义》和《JJF 1059-1999测量不确定度的评定与表示》对测量不确定度的定义是：测量不确定度是表征合理地赋予被测量之值的分散性，与测量结果相联系的参数。此参数可以是诸如标准偏差或其倍数，或说明了置信水准的区间的半宽度。此定义里的“合理”没有明确的定义和说明，怎样算是“合理”容易引起争议[14]。另外定义里的“相联系”一词表述不够准确，其实测量不确定度与测量结果并没有直接关联，只是与测量结果放在一起用来说明被测量真值所处的范围[15]。该定义与《JJG 1027-91测量误差及数据处理》相比，两者对不确定度的概念、评定方法均相同，表达形式也一样。只是《JJF 1059-1999测量不确定度的评定与表示》对B类不确定度的信息来源及测量值在常见分布下的计算方法更加具体，可操作性更强。另外，在报告最终测量结果时，要用扩展不确定度或合成标准不确定度表示，不再使用总不确定度这个术语。

2007年《VIM》第3版中测量不确定度的定义是：根据所用到的信息，表征赋予被测量量值分散性的非负参数[16]。定义中所用到的信息指与测量活动相关的测量仪器、方法、条件等提供的信息，包括检定证书、校准证书、文献资料、手册以及实践经验等。定义中，参数指标准测量不确定度的实验标准偏差或其倍数，或说明了包含概率的区间半宽度，表述比以前更规范、更科学。非负明确了测量不确定度恒为正值，这一点在以前是由注释说明的。因此，该定义较以前的定义，本质是相同的，表述更加科学。

4 结语

在测量过程中，误差是不可避免的。由于科学技术的发展和实际生产的需要，误差理论也在不断发展，《VIM》的定义和国家计量技术规范也随之变化，变化的趋势将更加科学，更具有可操作性。我们必须及时学习和掌握国际、国内的最新计量技术规范，才能掌握好处理测量和实验数据的方法，合理计算所得结果，在一定条件下得到更接近于真值的数据，对测量结果进行最准确可靠的评定。

参考文献:

[1] 费业泰. 误差理论与数据处理[M].5 版. 北京: 机械工业出版社, 2009.

[2] 耿维明.测量误差与不确定度评定讲座(一) 测量误差的概念及其分类[J].中国计量, 2010 (12) :68- 71.

[3] 费业泰. 误差理论的研究与进展[J].计量技术,1998(8): 40- 41.

[4] 罗振之, 施昌彦, 金华彰. JJF1001-1998通用计量术语及定义[S] . 北京: 中国计量出版社,1998.

[5] 金华彰.“计量”一词溯源回顾我国“计量”名词定义的制定[ J] . 中国计量, 2010(3) : 53- 56.

[6] 张成悌. 测量与计量的同异[J] . 中国计量, 2010(7) : 54- 55.

[7] 宣湘. 我国计量工作的现状和前景展望[EB/OL].[2006-07-21] (2011-06-20). http://www.jxzj.gov.cn/jxzj/ShowArticle.jsp?id= 9784.

[8] 金华彰. JJG1001-1982常用计量名词术语及定义[S].北京: 中国计量出版社, 1982.

[9] 鲁绍曾, 金华彰, 施昌彦. JJG1001-91通用计量名词及定义[S] . 北京: 中国计量出版社, 1991.

[10] 钱钟泰, 邹本霞. 我国的JJG1027-91”测量误差及数据处理”技术规范及其解说与1993年7个国际组织的”测量不确定度表示指南”[J] . 中国计量,1997(3) : 49-51.

[11] 李慎安, 钱钟泰, 刘智敏, 等. JJG1027-91测量误差及数据处理(试行) [S] . 北京: 中国计量出版社, 1991.

[12] 李慎安, 施昌彦, 刘 风. JJF1059-1999测量不确定度的评定与表示[S] . 北京: 中国计量出版社, 1999.

[13] 李慎安. 有关测量误差的几个基本术语的新定义与有关问题[J] . 计量技术, 1998(4) : 40-42.

[14] 李慎安. 测量不确定度的定义及其有关问题[J].计量技术, 1999(6) : 47- 50.

[15] 李慎安. 有关不确定度的概念与术语[J].中国计量,2000(3): 49-51.

[16] 耿维明. 测量不确定度的概念[J].中国计量, 2011(1):68- 69.